Od Pitagore do Einsteina, najpoznatije matematičke jednačine oblikovale su način na koji razumijemo svijet. Iako mnogi matematiku vide kao apstraktnu i tešku, iza nje se krije neiscrpan izvor logike, ljepote i otkrića.
Kroz nekoliko primjera ćemo pokazati kako su jednačine iz matematike promijenile svijet: od jednostavnih geometrijskih formula do teorija koje objašnjavaju svemir, haos i energiju. Iako su Maxwellove i Schrödingerove jednačine temelj kvantne fizike, matematika ima ogroman značaj i u mnogo prizemnijim stvarima. Da biste se uvjerili koliko često koristite matematiku, pogledajte naš pregled o tome koja je korist od matematike u svakodnevnici.
Čista matematika je, na svoj način, poezija ideja logike.
Albert Einstein

Ko je “izmislio” jednačine?
Ideja matematičke jednačine datira još iz starog Egipta i Babilona, ali pravi oblik dobija tek u antičkoj Grčkoj. Pitagora je prvi postavio koncept matematičkog dokaza, dok su arapski naučnici poput Al-Khwarizmija (od čijeg imena potječe riječ algoritam) razvili algebru, ključni alat za rješavanje jednačina.
Danas, gotovo svaka oblast nauke – od fizike do ekonomije – koristi principe koje su oni postavili prije više od 2000 godina.
| 🙋♂️Jednačina | 🔢 Naziv jednačine ili teorije | 🔎 Šta objašnjava / čemu služi |
| a2 + b2 = c2 | Pitagorina teorema | Pomaže u rješavanju problema koji uključuju prave uglove. |
| F = G * (m₁ * m₂) / r² | Univerzalni zakon gravitacije | Objašnjava da se dva tijela u svemiru privlače silom koja zavisi od njihove mase i udaljenosti između njih. |
| E = mc2 | Teorija relativnosti | Objašnjava osnovni odnos između prostora, vremena i gravitacije. |
| A = π * r² | Površina kruga | Izračunava površinu kruga. Također pomaže u mjerenju valnih oblika, zakrivljenosti sočiva i raspodjeli svjetlosti. |
| xₙ₊₁ = r * xₙ * (1 - xₙ) | Teorija haosa | Koristi se za razumijevanje i predviđanje ponašanja složenih sistema koji su osjetljivi na početne uslove. |
| e^(iπ) + 1 = 0 | Eulerova identiteta | Korisna u analizi valova i oscilacija. Povezuje različite oblasti matematike. |
| ΔS = ∫(dQ / T) | Drugi zakon termodinamike | Određuje smjer prijenosa potencijalne energije. |
| iħ * ∂ψ/∂t = Ĥψ | Schrödingerova jednačina | Opisuje talasne funkcije nerelativističkih kvantno-mehaničkih sistema. |
| ∇ · E = ρ / ε₀ ∇ · B = 0 ∇ × E = -∂B/∂t ∇ × B = μ₀J + μ₀ε₀(∂E/∂t) | Maxwellove jednačine | Osnova su klasične elektromagnetike, optike te električnih i magnetnih krugova. |
Pitagorina teorema: osnova svih osnova
Formula: a² + b² = c²
Pitagorina teorema je jedna od najpoznatijih matematičkih jednačina svih vremena. Nastala oko 530. godine prije nove ere, ova formula i danas ima praktičnu primjenu – od građevinarstva do arhitekture.
Kroz nju učimo kako pravougli trougao funkcioniše, ali i kako se geometrija primjenjuje u svakodnevnim situacijama:
- prilikom mjerenja visine zgrade bez penjanja,
- kod kreiranja 3D modela,
- u dizajnu mostova i konstrukcija.
Jeste li znali?
Pitagorejci su vjerovali da se kroz brojeve može objasniti cijeli svemir — što je jedan od prvih filozofskih temelja matematike.
Pitagorina teorema: Simbol veze između geometrije i stvarnog svijeta. (Izvor:
Univerzalni zakon gravitacije
Formula: F = G * (m₁ * m₂) / r²
Isaac Newton je u 17. stoljeću prvi objasnio kako se svaka dva tijela u svemiru privlače. Ova jednostavna matematička jednačina promijenila je način na koji posmatramo planete, Mjesec, pa čak i pad jabuke na Zemlju.
Ona nas uči da matematika nije samo apstraktna, već konkretan način da opišemo sile koje oblikuju svijet oko nas.

Gravitacija: Nevidljiva sila koju je Newton pretvorio u brojke. (Izvor: Pixabay.com)
Teorija relativnosti: kada vrijeme nije isto za sve
Formula: E = mc²
Ova jednostavna, ali moćna formula Alberta Einsteina pokazala je da su masa i energija međusobno povezane. Danas je temelj fizike, nuklearne energije i astrofizike.
Mašta je važnija od znanja. Znanje je ograničeno, a mašta obuhvata cijeli svijet.
Albert Einstein
Einsteinov rad pokazuje da su matematičke jednačine most između mašte i stvarnosti. Za širi kontekst primjene logike i analize u ličnom životu i karijeri, pročitajte i zašto je važnost matematike u svakodnevnom životu sve veća.
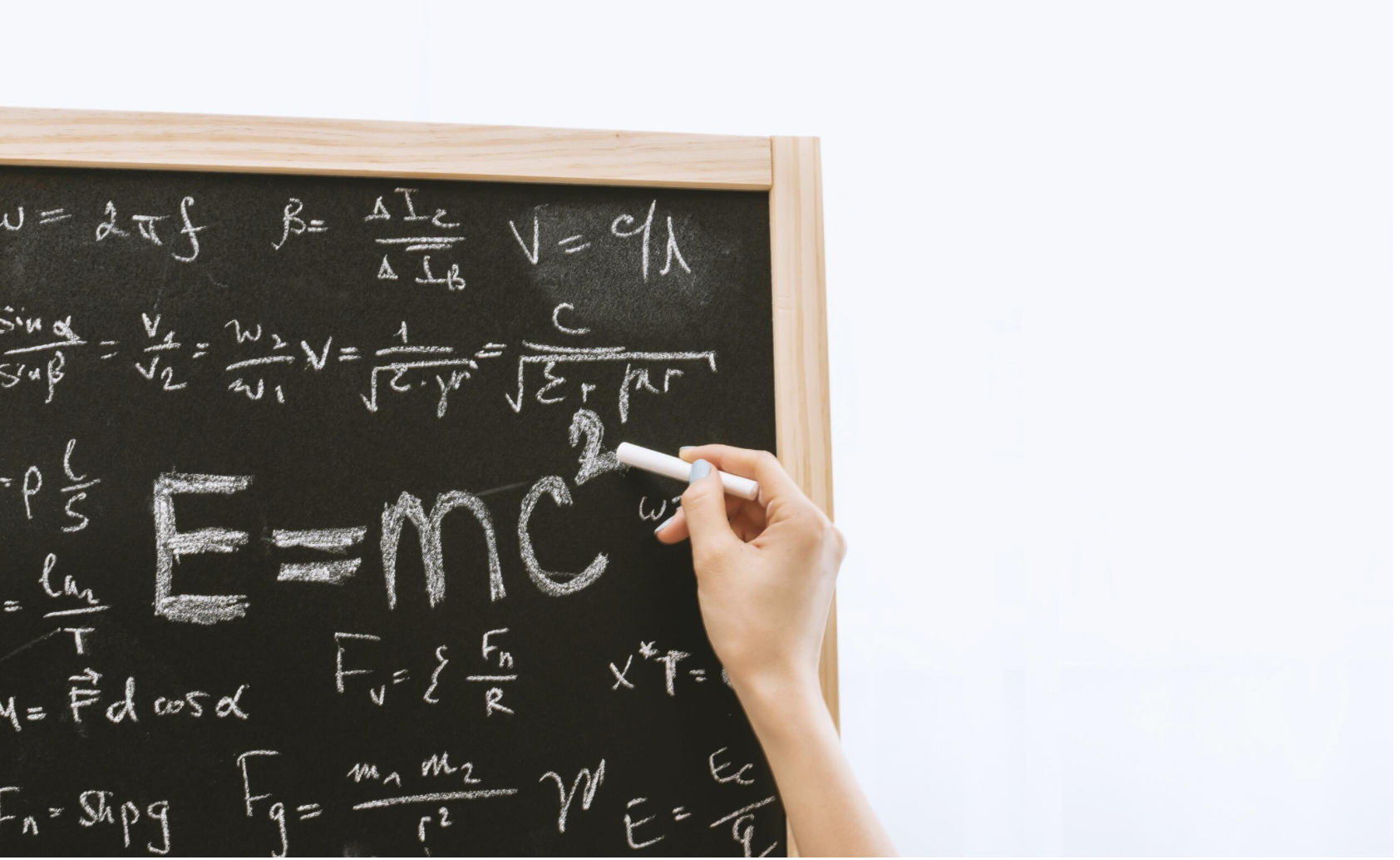
Teorija relativnosti: Način na koji razumijemo prostor, vrijeme i energiju. (Izvor: Pexels.com - jeshoots.com)
Teorija haosa i "efekat leptira"
Teorija haosa objašnjava da i najmanja promjena na početku može dovesti do ogromnih posljedica.
To je ono što se popularno naziva "efekat leptira", odnosno ideja da leptir koji mahne krilima u Brazilu može izazvati oluju u Aziji.
U matematici, teorija haosa koristi fraktale i nelinearne jednačine kako bi opisala složene sisteme poput vremena, tržišta, mozga ili ekosistema. Kroz ove složene sisteme, najbolje se mogu razumjeti i ilustrovati teorija haosa primjeri iz stvarnog svijeta.
Eulerova identiteta: "najljepša jednačina na svijetu"
Formula: e^(iπ) + 1 = 0
Leonhard Euler, švicarski matematičar, stvorio je ono što mnogi smatraju najljepšom matematičkom formulom ikada. U jednoj elegantnoj liniji povezao je pet temeljnih brojeva:
- e (bazu prirodnog logaritma)
- i (imaginarni broj)
- π (pi)
- 1 i 0 (osnove brojevnog sistema)
Ova formula simbolizuje čistu harmoniju matematike – dokaz da apstraktne ideje mogu biti i estetski zadivljujuće.
Eulerova identiteta: Savršena kombinacija logike, jednostavnosti i ljepote. (Izvor: Youtube.com - 3Blue1Brown)

Površina kruga
Krug je zatvorena, ravna linija kod koje su sve tačke jednako udaljene od središta. Jednostavnije rečeno, krug je zatvorena linija poput prstena ili gume.
Formula za površinu kruga:
A = π * r²gdje je:
- A = površina kruga
- π (pi) = 3,1416
- r = poluprečnik kruga
Poluprečnik predstavlja udaljenost između središnje tačke kruga i bilo koje tačke na njegovoj ivici.
Bez obzira koristi li se u praktične svrhe ili u fizičkim proračunima, poznavanje formule za izračunavanje površine kruga je od suštinskog značaja. Zahvaljujući ovoj poznatoj matematičkoj jednačini, možemo dublje proučavati pojave poput talasa, elektromagnetnih polja, sočiva i raspodjele svjetlosti.
Drugi zakon termodinamike
Prvi zakon termodinamike definiše da se energija između fizičkih sistema može razmjenjivati u obliku toplote i rada.
Drugi zakon uvodi novu veličinu poznatu kao entropija, odnosno princip promjene koji određuje u kojem smjeru su moguće transformacije potencijalne energije.
Toplina uvijek teče od toplog ka hladnom – suština drugog zakona termodinamike. (Izvor: Youtube.com - The Royal Institution)
Ovaj zakon navodi da nije moguće da jedini rezultat nekog procesa bude prenos toplote s hladnijeg tijela na toplije. Drugim riječima, toplota se uvijek prirodno prenosi od toplijeg ka hladnijem tijelu, a ne obrnuto.
Drugi zakon termodinamike predstavlja fizički princip koji postavlja ograničenja u smjeru prenosa toplote između tijela. Još 1873. godine, Ludwig Boltzmann i Max Planck razvili su ovu teoriju, polazeći od eksperimentalnih činjenica i njihovih generalizacija, čime su postavili temelje moderne termodinamike.
Formula:
ΔS = ∫(dQ / T)gdje je:
- ΔS = promjena entropije
- dQ = količina prenesene toplote
- T = apsolutna temperatura na kojoj se prenos odvija
Ova formula opisuje kako se entropija, odnosno stepen nereda u sistemu, mijenja u zavisnosti od količine toplote i temperature.
Da bismo ovaj zakon razumjeli u praksi, dovoljno je zamisliti čašu s ledom. Tokom vremena, led se topi, ali ne može sam od sebe zamrznuti piće. Toplota se, prema drugom zakonu termodinamike, uvijek prenosi od toplijeg prema hladnijem tijelu — nikada obrnuto.
Schrödingerova jednačina
Austrijski fizičar Erwin Schrödinger imao je brojne briljantne ideje, a među njima i poznati misaoni eksperiment o "mački koja je istovremeno živa i mrtva". Bez obzira na njegovu sklonost filozofiji i paradoksima, upravo je on zaslužan za jednu od najpoznatijih formula kvantne mehanike.
Schrödingerova jednačina ključna je za razumijevanje načina na koji se čestice mijenjaju tokom vremena. Pomaže da opišemo različita stanja u kojima se čestica može nalaziti, bilo da je riječ o atomima, elektronima ili talasima energije.

Schrödingerova mačka: Metafora kvantne neizvjesnosti i paradoksa između stvarnosti i promatranja. (Izvor: Pixabay.com - Gerd Altmann)
Ova jednačina postavlja i jedno duboko filozofsko pitanje: Postoji li materija samo u fizičkim stanjima koja možemo vidjeti (čvrsto, tečno, gasovito)?
Na filozofskom nivou, Schrödingerova jednačina nas podstiče da promislimo o prirodi materije i percepciji stvarnosti. S praktične strane, imala je ogroman značaj za razvoj nuklearne energije, računarske tehnologije i laserskih sistema.
Maxwellove jednačine
Četiri Maxwellove jednačine čine jedan od najvažnijih temelja savremene fizike. Ove formule su od ključnog značaja za razvoj elektrodinamike i teorije relativnosti, a predstavljaju most između električnih i magnetnih polja.
Zanimljivo je da se svake godine objavi više od 30.000 naučnih radova iz oblasti matematike i fizike, a značajan broj njih koristi barem jednu od ovih jednačina. Smatra se da su Maxwellove jednačine vrhunac klasične fizike, jer se iz njih mogu izvesti sve druge formule koje se koriste za proračune u elektromagnetizmu.
Kako zapravo 'izgleda' elektromagnetno polje? Pogledaj kako Maxwellove jednačine oživljavaju kroz jednostavne i dinamične vizuale. (Izvor: Youtube.com - The Science Asylum)
Ove jednačine opisuju međusobnu interakciju električnih i magnetnih polja i njihovu povezanost s električnim nabojima. I električna i magnetna polja mogu se vizualno prikazati pomoću dijagrama silnica, koji ilustriraju njihov smjer i intenzitet.
Maxwellove jednačine nisu samo temelj moderne fizike, već i dokaz da je matematika nerazdvojni dio našeg društva, od rada električnih uređaja i telekomunikacija, do svjetlosti, optike i svih oblika moderne tehnologije. O ovim temeljima moderne ekonomije govori naš članak o važnosti digitalne matematike.
Matematika u svakodnevnom životu
Iza svake teorije krije se praktična primjena:
- u tehnologiji, algoritmi zasnovani na matematici pokreću naše telefone i društvene mreže,
- u ekonomiji, jednačine predviđaju trendove tržišta,
- u umjetnosti, zlatni presjek (φ = 1.618) određuje proporcije remek-djela,
- u prirodi, Fibonacci niz opisuje oblik školjki, cvjetova i galaksija.

Zlatni presjek: Dokaz da se matematika nalazi i u prirodi i u umjetnosti. (Izvor: Pexels.com - Arndt-Peter Bergfeld)
Trikovi i zanimljivosti za ljubitelje matematike
Jeste li znali?
- Broj 9 je magičan: zbroj svih njegovih višekratnika uvijek vraća broj 9 (npr. 2×9=18 → 1+8=9).
- Svi parni brojevi završavaju se na 0, 2, 4, 6 ili 8: to znači da se mogu podijeliti s 2 bez ostatka.
- Ljubitelji logike znaju: ako rješavaš sudoku, zapravo vježbaš osnovne koncepte kombinatorike i teorije vjerovatnoće! Želite li se dodatno zabaviti i oštriti um, preporučujemo vam i naš izbor matematičkih zagonetki i mozgalica.
Matematika može biti zabavna: Sve je u načinu na koji joj pristupimo. (Izvor: Pixabay.com - Chuk Yong)
Zaključak: Ljubav prema matematici nije mit
Matematičke jednačine nisu samo simboli na papiru. One su priče o otkrićima, radoznalosti i ljudskoj potrebi da razumijemo svijet.
Bilo da istražuješ Pitagorinu teoremu, teoriju haosa ili ljepotu Eulerove identitete, svaka od njih skriva duboku lekciju o povezanosti svijeta i logici prirode.
Ako i ti želiš otkriti tu ljepotu u praksi, počni rješavati zadatke i jednačine iz matematike svakog dana, jer iza svakog broja stoji ideja, a iza svake ideje mogućnost da promijeniš svijet.
Sažmi uz pomoć AI















